構成(論)的手法、構成(論)的アプローチ、Constructive Approach
更新: 2012.08.14 Masa, Download PDF: ca.pdf
■ 注意
ここで説明している内容は、私の研究分野の関係で「生命科学」「生物学」「数理モデル」「計算モデル」を想定した話が中心になっています(が社会科学や認知科学のモデルなど他のモデルの話にも拡張して理解できるとは思います)。「論」が入る場合と入らない場合の両方が使われているようですがどちらもほぼ同じ意味でここでは「構成的手法」という呼び方で統一します。
■ 概要
構成的手法とは科学的研究手法の一つで
対象を観察・分析し、記述するという従来の科学的方法と相補的なもので、簡単に言うならば、システムを作って動かすことにより理解しようという方法
であると橋本敬教授は説明しています[knowledge02](構成論的手法)。もう少し形式的に一般化して言い換えると、
研究対象のモデルを構成することで、ある論理を実現するための十分条件を示す方法
であると言えます。つまり、その論理を実現するために必ずしもその条件が必要とは限らないが、その条件であれば目的の論理を実現することが可能、といった条件を示すことになります。「条件」といっても、初期値や境界条件、パラメータに限らず、モデルの物理構造や論理構造などのアーキテクチャも含みます。
生命の起源研究でユーリとミラーのフラスコ内でのアミノ酸合成実験[miller1953]は有名ですが、彼らは
- 無機物から有機物を合成する原始地球環境のモデルを構成して
- 無機物から有機物を合成する一つの条件(可能な論理)を示しました
原始地球上で実際に無機物から有機物が合成されたかどうかは別として、モデルを構成して無機物から有機物を合成するための十分条件を示した、という意味で構成的研究であると見なせると思います。さらに、ただ単に「作りました」というだけでなく、その構成する条件を形式化できたことが、構成的手法の特筆すべき効果であると言えます。つまり、論理を形式化することで、それを「原始地球上でこれこれこういう条件が成り立っていれば、こういう無機物からこういう有機物が合成されたかもしれない」という現実世界の現象に対して具体的な仮説として提示できることにつながります。そして、その仮説は地質学などの別の方法で検証することが可能になります。金子邦彦教授は構成的手法を可能な論理を構築する一つの手段として説明していて、構成的研究を次の3つに分類しています。
- 純粋思考実験
- コンピュータ付き思考実験
- 実験室における構成実験
特に、2. コンピュータ付き思考実験は論理的な思考では到達しがたい直感を獲得するために有用だと述べています[kaneko09]。近年生物学の分野で「合成生物学(Synthetic biology)」「構成的生物学(Constructive biology)」といった分野が成長しつつあり、これらは基本的に構成的手法を用いた研究であると言えるでしょう。
■ 通常のモデル研究との違い
一般的に「モデル」とは、対象とするシステムを簡略化して、その本質を表したもののこと(引用Wikipedia「数理モデル」)で、数理モデル、計算モデル、実験モデル、などを指します。自然科学一般において、モデルを用いて何かの自然現象を理解したいという場合は通常はモデルの妥当性(model validation)を検証(確認、評価)する必要があります。前述の橋本教授の説明で一つ注意すべき点はシステムを作って動かすことで直接的に理解できるのは作られたシステムそのものであって、もしそのシステムが何か実在するものや現象を元に構成されているモデルだとして、その実在の対象を理解したいという場合は、そのシステムが実際の対象のモデルであることを確かめるステップが必要になります。つまり、そのモデルが実際の現象をどれだけ表現できているかを確かめる過程です。普通は他の実験結果や観察結果と比較することでモデルの妥当性を検証します。そして、モデルが現実の対象の一部を適切に表現できていると考えられる場合、モデルの性質や動作原理などを調べて、その現実の対象の動作を予測したり、その対象の動作メカニズムを解明したりします。
この通常のモデル研究はモデルを構成するという意味において構成的手法の一種だと考えられますが、構成的手法によるモデル化という場合は普通、さらに一般化して現実にない対象物や現象をも含みます。それは、現実に起きている現象を再現するモデルの構成というより、
ある特定の機能/論理を実現するためにはどのような条件が必要か
という問いに答えるためのモデル構成だからです。現実世界に比較対象が実在しないモデルの場合そもそも上記の「モデルの妥当性」を検証することが不可能な場合もあり得ます。例えば、力学系の「ローレンツモデル」はある大気変動モデルを極度に抽象化しているため、現実の特定の対象物と比較すること自体があまり意味をなしません。しかし、単純化したモデルを構成したからこそ、気象モデルのカオス的振る舞いの発見につながりました。この場合は、現実に起きている何かの現象のモデル、というよりカオス的振る舞いを実現する力学系のモデルと言うことができるでしょう。その意味で「カオス力学系のモデル」としては妥当かどうかを検証することは可能です。橋本敬教授はジョン・フォン・ノイマン(1903 - 1957)の自己複製オートマトンの研究を例に解説しています[knowledge02](構成論的手法)。フォン・ノイマンは自己複製するセルオートマトンモデルを構成して、自己複製の可能な論理を構成しました[sato10]。このモデルは現実世界の具体的な対象物をモデル化したものではなく、自己複製の論理を構築する、という目的で作られたと考えることができます。つまりフォン・ノイマンが構成したのは自己複製の一つのモデルだと言えます。これらのモデルは、現象を再現する現象論的モデルという呼び方に対して、ある種の論理を再現する理論的モデルと呼べるかもしれません。有田隆也教授はこのように現実の現象と対比できないようなモデルを「概念レベルのモデル」として分類しています[arita08]。しかし、構成されたモデルをどう呼ぶかというのは本質的な問題ではなく、そのモデルがどのような目的で構成されたのか、またそのモデルを示すことでどのようなことがわかるのか、といったモデル構成の意義を考えることが重要だと思います。金子教授の本から引用すると「われわれは、今ある生物の詳細を調べて、それを作っている非常に良くできた設計図を探ろうとするのではなく、生物システム一般に当てはまる性質を探りたい。そのためには今存在する生物にあまりこだわらず、最低限だけ現生物と共有するシステムを構成してみて、そこでこれらの性質が現れるかをみるのが有効であろう。これがここで考える構成的方法、構成的生物学である」と言われています[kaneko09, Chap2-1]。つまり、ここで言っているモデルを構成する意義というのは「生物システム一般に当てはまる普遍的な性質を調べるため」であり、ある性質を実現するための最低限の枠組み(モデル)を構築する、というのは上述したように「ある論理実現のための十分条件を示すためのモデル構成」だと言えるでしょう。
■ 構成するための条件がわからないのに構成できることの矛盾
上記の構成的手法の説明には、
構成するための条件が既知でないのにどうやって構成するのか?
という矛盾が含まれます。この疑問についての回答は(個人的経験に基づいて端的に言えば)「試行錯誤と経験による方法」になります。といっても、闇雲にとにかく作ってみる、という訳ではなく、先行研究や既存のアイデアから、プロトタイプ的なモデルを構成して、そのシミュレーション結果の分析から論理構築/モデル構築に何が足りないのか、といったことを考え、モデルを作り替え、再シミュレーションして、ディスカッションして、モデル再構築、といった作業を繰り返しながら、目的の機能/論理を実現していきます。モデルを作り替えるときには既存の理論や近似手法、工学的な手法なども使えるかもしれません。この過程が橋本敬教授の言うところの「作って動かす」ことの一つ目の意味になると思います。シミュレーションと言ってもコンピュータシミュレーションに限らず、実際の実験なども含みます。この方法はソフトウェア開発のプロトタイピング手法に似ており、コンピュータシミュレーションデモルや計算モデルを構築する場合はいわゆる「アジャイル開発手法/反復型開発手法」を構成的手法に適用できる可能性が高いと言えます。特にソフトウェア開発を支援するツールやフリーのプロジェクト管理ツールなど良いものがたくさん出回っていますので、これらを研究活動に活用しない手はありません。またこのように試行錯誤的にモデル再構成を繰り返すということは、必然的に何度も失敗することが前提になります。そういった意味では、実験室での構成実験の前に、計算モデルでの構成的研究が有効に機能すると思われます。
橋本敬教授はこの疑問に対しては「進化的構成的手法(Evolutionary Constructive Approach)」という手法を提案しています[hash08]。端的に言うと、進化的アルゴリズムや学習アルゴリズムを用いてシステムを進化/発展させることによって、設計図なしにモデルを構成していくという手法です。ただし、進化的アルゴリズムや学習アルゴリズムの設計、また進化させるシステムの元になるシステムの設計は必要になると思われます。
ここでは、科学的研究の場において一般的に用いられていると考えられる仮説演繹法と構成的手法との関連を考えてみます。
まずその前に、推論の方法を整理しておきます。物事を推論する方法として演繹(deduction)と帰納(Induction)があります。
演繹的推論
演繹とは三段論法に代表されるようにいくつかの論理的規則をもとに前提から結論を順に導く方法です。例えば、
A → B (A ならば B)
B → C (B ならば C)
この二つの論理的規則から
A → C (A ならば C)
という関係を導く方法です。ここで、A、B、Cは「命題」と呼ばれるもので「○○は××である」といった「真偽」(正しいか正しくないか、成立するかしないか)を問える形の条件文になります。「A → B」のAを前提、Bを結論、と言います。「→」は命題論理における論理包含を表す論理記号で、日本語ならばよく「ならば」と表現されます。また「A → B」は「論理式」とよばれ、これも真か偽かを問える「命題」となります。日本語では「Aが真であるならBも真である」と解釈される命題になりますが、注意する点は「Aが真でない」場合、Bが真であろうが偽であろうが「A → B」という命題は常に「真」になる点です(ここが「ならば」という訳を使った場合の直感からずれるところです)。つまり、演繹的推論において「A → B」という命題が信頼できる規則だとしても、前提が成り立たなければ、結論に関して正しいとも間違っているとも主張できないことになります。真偽値表で表すと以下のようになります。
| A |
B |
A→B |
| T |
T |
T |
| T |
F |
F |
| F |
T |
T |
| F |
F |
T |
T は「True(真)」、Fは「False(偽)」を表しています。ちなみにこのとき、命題「A」を「Bが成り立つための十分条件(Sufficient Condition)」、命題「B」を「Aが成り立つための必要条件(Necessary Condition)」と言います。簡単な例を使って説明すると
それはりんごである → それは果物である
という論理式の場合、「それがりんごである」ことは「それが果物である」ための「十分条件」であり、「それが果物である」ことは「それがリンゴである」ことの「必要条件」となります。「必要条件」は「十分条件」
を包含している、と言えます。条件の集合をベン図で表現すると下図のようになります。
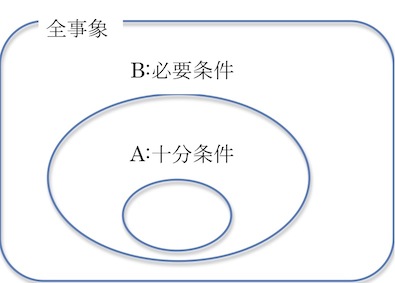
つまり、果物にはリンゴ以外にもぶどうやみかんやその他いろいろありますが、リンゴは野菜でもなく肉でもなく果物であることが確定しています。別の言い方をすると、それがリンゴであるとわかれば必ず果物であると言えますが、それが果物だとわかったからといってリンゴである保証はありません。つまり、この場合は「逆」
それは果物である → それはりんごである
という論理式は成り立ちません(偽である、と言えます)。
帰納的推論
帰納とは観察される現象から共通する一般法則を導く方法で
人間Aは死んだ
人間Bは死んだ
といった事実が観察されたことから
すべての人間は死ぬ
というような関係(一般法則)を推論することです(厳密には枚挙的帰納法と言います)。帰納的推論は論理的推論ではないので厳密には論理式で表すことができませんが、三段論法で用いられる
A → B(大前提、仮説)
B → C(小前提、事例)
A → C(結論、結果)
という論理式をあえて用いて表すと
B → C(小前提、事例)
A → C(結論、結果)
という観測事実から
A → B(大前提、仮説)
という一般法則を導く(推論する)ものだと言えます。注意すべき点は、演繹的推論の結果は(前提が真ならば)必ず真になりますが、帰納的推論の結果はすべての事例を枚挙しない限りはいくら観察事実を枚挙したところで必ずしも真とは言えないところです(全称命題の場合は、たった一つの反例で仮説が成り立たなくなります)。良く例として出されるのは黒いカラスの命題で、地球上の一万羽のカラスの色を調べてすべてが黒だったからといって「カラスは黒い」という命題が真であると言うことはできません。地球上のすべてのカラスを調べない限り白いカラスがどこかにいるという可能性はなくならないからです(ちなみに余談ですが白いカラスは実在しています)。
仮説演繹法
仮説演繹法は、ある仮説「A→B」に基づき、前提Aから演繹的に推論した結論Bと、仮説の前提と同じと見なせる同様の前提A'のもとで実際に実験(観察)した結果B'とを比較して、同等だと解釈できるなら
A → B (仮説)
が確からしい、という主張する方法です。
(仮説)A → B
| 比較
(実験)A' → B'
一つ(もしくは複数)の実験(観察)結果をもってして仮説が正しい(そうだ)、と推論する訳ですから、一種の帰納法と考えられます。仮説演繹法の欠点は枚挙的帰納法と同じく、数多くの実験をして観測事実として前提Aから結論Bを得たからといって必ずしも「 A → B」 の法則が成り立っているとは限らない、というところです(枚挙的帰納法と同じくたった一つの反例で仮説が真とは言えなくなる場合があります)。いくら実験をしてもたまたま偶然に、その法則に従った(ように見える)結果が得られているだけ、という可能性はなくならないからです。しかし、その仮説が反証されるまではとりあえず、信用できそうなものとしておいておきましょう、あるいは、ある条件下ではその仮説は信用できるものとしておきましょう、というのが現在の多くの科学者、研究者の立場だと思います。例えば、ニュートン力学はいつでもどこでも成り立つ絶対的な法則ではなく、電子や素粒子などの量子スケールのレベルでは成り立たず「日常的なスケールでは有効な理論」だと考えられています(引用Wikipedia「ニュートン力学」)。
一般的にモデルを用いて実際の現象を予測(推論)する場合は、基本的にはこの「仮説演繹法」に従っていると考えられます。つまりモデル自体が「仮説」であり、ある条件でモデルをシミュレーションした結果が、現実の実験(観察)結果と同じになった(と解釈できる)なら、どうもそのモデルはある現実の現象モデルとして妥当だと、主張するものです。
(モデル)A -(シミュレーション)→ B
| 比較
(実験) A' -------------------→ B'
これはつまり先に述べた「モデルの妥当性検証」そのものになります。注意するべき点は、仮説演繹法の欠点と同じく、いくらモデルの振る舞いと現実の振る舞いが同じだ(と解釈できる)からといって、必ずしも現実の対象物がそのモデルと同じメカニズムで動いているという訳ではないという点です(そのモデルが有効でない可能性はなくならないので)。ただし、ある程度モデルの妥当性が検証されれば、その後実際の実験や観察をする代わりにモデルを用いて研究を進めることで実際の対象物や現象の理解につながります。例えば、人間の代わりにマウスをモデルとして使って薬の効果を調べたり、ナビエ-ストークス方程式を計算して津波のでき方を調べたり、といったことに相当します。マウスで効いた薬が必ずしも人間に有効だとは限りませんが、ある程度はその効果を調べることができる我々は信じています。それはマウスが人間のモデルとして妥当だと検証済みだからです。同様にナビエ-ストークス方程式を計算することで津波のでき方を調べられる(と信じられる)のはナビエ-ストークス方程式が流体のモデルとして妥当だと検証済みだからです。
構成的手法によるモデル化とアブダクション
構成的手法によるモデル化においても
A → B(モデル、仮説)
という論理が成り立つことをモデルを構成することで検証した、ことになるので仮説演繹法であるとは言えます。しかし、ある現象を再現するモデルであることを検証した、というよりは、
ある論理が成り立つことをモデル構成を通して検証した
ということになります。ただ、構成的手法によるモデル化という場合、上記の「論理の検証」というよりはむしろ
A → B(モデル、論理)
という論理がモデル上で成り立つことを示すことで
Bという現象/機能を実現するためにはAが十分条件となる
ということを示すことが、構成的手法によるモデル化の第一義的な目的になります(ただし、Aは十分条件であるので、A以外の条件でもBを実現することができる可能性は残りつづけます)。
もう一度言っておきますが、モデルの元になった実在のシステムについてこの論理が成り立つかどうかは、また別の問題になります。
そして、目的のモデルが構成された後、現実の問題に還元する場面では(例えば自然科学的、社会科学的にモデルの意義を見いだすためには)「現象を再現するモデルを構築して現象を理解する」という側面よりは、「構築した論理(モデル)から現実の現象に対する仮説を生成する」という側面が強調されます。つまり、もしBと同じようなだと解釈できる現象が現実に起きているとして、この論理(モデル)から逆に
現実的にもBという現象を実現するためにAという条件が使われている(成り立っている)のではないか
と予想する(仮説を立てる)ことです。ここの「条件」は最初に述べたように「十分条件」の意味で温度や圧力といったパラメータや境界条件に限らずモデルで用いられている論理やアーキテクチャなども含まれます。もちろんこれが正しいという保証はありませんが、今までに示されたことがない論理ならば、確かめてみる価値は生まれます。またモデルが構築されている分、仮説の形式化もしやすく、問題点をはっきり問えます。これは結論と一般法則から前提を推論することに相当し「アブダクション」「仮説的推論」などと呼ばれています(形式論理的には「後件肯定の誤謬」と言われていて、論理的には妥当でない推論になります)[yonemori07]。このことから橋本敬教授らは構成的手法によって新しく仮説を生成することできるということを指し「構成的シミュレーションはアブダクションエンジンである」と言っています[hash10]。リンゴの例について説明すると、
それはりんごである → それは果物である
この逆は必ずしも成り立つとは限りませんが、場合によっては成り立つこともありえます。つまり、この論理式が信頼でき、かつ、それが果物であるとわかった場合、絶対にリンゴであるとは言えませんが、場合によってはたまたまリンゴかも知れない、と言うことはできます。そして、それがリンゴかどうかを確かめるには、色を見たり、形を見たり、味を調べたり、DNA配列を調べたり、と他の方法で検証していくことになります。
ユーリとミラーのアミノ酸合成実験に照らし合わせて考えてみると、実験は(論理式的に簡単に記述すると)
水、メタン、アンモニア、水素 + 放電 → アミノ酸
という図式で表せますが、この論理から、前提部分の
1. これらの物質(水、メタン、アンモニア、水素)が反応ができるくらい十分に存在している
2. 放電に相当するエネルギー供給源がある
ということが原始地球上で成り立っていたかどうかが現実の現象に対する検証するべき仮説になります。そしてその仮説は地層を調べたり、原始地球の形成過程を調べたり、と別の方法で検証していくことができます。いくら実験室で原始地球のモデルを構成しても、原始地球で起きたことを検証できるわけではありません。まして原始地球上でおきた化学反応を明らかにした訳でもありません。原始地球で起きた(かもしれない)論理の可能性を仮説として提示できるだけです。ここを注意しなくてはいけません。しかし、さまざまなモデルを構成したり、さまざまな観測事実からその仮説を検証して、仮説の信頼性を向上させること(もしくは、その前提が成り立たない条件を示したり、反例を見つけて、反証すること)はできるとは思います。
構成的手法による研究では、ある一つの対象に対してさまざまな側面から構成的モデルを構築することが十分条件を絞っていく、つまり必要十分条件に近づけていく一つの手段になります。例えば、構成的モデル化によってある現象、機能についていくつかの論理が得られたとします。
それはりんごである → それは果物である
それはぶどうである → それは果物である
それはみかんである → それは果物である
そうするとこれらの十分条件「りんご」「ぶどう」「みかん」の共通項を探ることで「果物」であることの必要十分条件を見つけることにつながります。例えば
それは受粉した雌しべの子房が発達した部分と、その付属器官である ←→ それは果物である
というふうに。つまり、構成的モデル化では単一のモデルを示して一つの十分条件を提示するだけではなく、何通りものモデル化を通して対象の必要十分条件を見つけていくことが重要であると思います。
■ 構成的手法の苦悩と効用
徐々に構成的手法を標榜する研究も増えてきて、一見すると魅力的な方法に思えるかもしれませんが、実際のところはまだ十分に形式化されているわけではなく、研究者の間でもそれぞれの哲学と経験に基づいて試行錯誤的に研究を進めているのが現状だと思います。ここまで述べてきたように、構成的手法を用いることによって新しい論理の発見が期待できるので、まだ基礎理論や基礎方程式の完成していないような新しい分野を開拓しようとするときに構成的手法は威力を発揮すると思われます。ここでは構成的手法によって何かの論理を構築しようとしたときの陥りやすい苦悩?と効用?をいくつか挙げておきます。
1. 目的の状態がそもそも不明
先ほどから
A → B
という論理式をもとに説明をしてきましたが、現実的には、そもそもBとはどういう状態を意味するのかすら不明な(形式化が難しい)場合があります。その典型的な例が「人工生命モデル」で、当初、作ることで生命の本質を理解しよう、ということで盛り上がった?と思いますが、そもそも最終的に作られるであろう「生命」もしくは「生命の状態、振る舞い」とはどういうものであるかがはっきり定義できません。しかし、そういったモデル化の過程や議論を通して「生命とは何か」「生命的振る舞いとはどういうものか」という議論が深まっていったことは間違いないはずで、科学的に意義はあったとは思います。むしろ、構成的手法によるモデル化の過程を通して、実現したい論理の形式化が進んだ、と考えることができます。フォン・ノイマンの自己複製オートマトンモデルは、現実の何かの現象をモデル化したものではないですが、自己複製の一つのアルゴリズムが示され、DNA分子複製の仕組み理解への示唆を与えたという意味で、自然科学的、生物学的にも意義があったはずです。
2. 論理が自明
例えば、ユーリとミラーの実験で、アミノ酸を最終的に得たいからと言って、タンパク質(アミノ酸が多数結合したもの)をタンパク質分解酵素を使って分解しても、なんら意味がありません(アミノ酸が存在しなければ、タンパク質も存在しないので、原始地球のモデルとしては意味がない。効率的に分解できる新しい酵素を発見した、という場合は別の意義があるかもしれませんが)。つまり、自明な論理に基づいてモデルを構成しても、そもそも構成的手法によるモデル化の意味がないと言えます。今までに示されたことがない論理を初めて示すから、モデルを構成することに意義が生まれる、ということです。
3. モデル化の問題
実現したい論理を、どのような条件(モデル)に帰着させるか、というのは難しい問題です。ある現象から、モデルを構成するということは数学的には逆問題に相当します。しかし、システムが決定していて出力値から入力値を再現するパラメータを推定する、というようなものではなく、構成的モデル化という場合は、システムそのものをどうやって実現するか、ということが問題になる場合が多いので、その探索空間は果てしなく広いと言えます。例えば、水の運動を理解したいというときに、ニュートン力学に基づくモデルを考えるのか、量子力学に基づくモデルを考えるのか、流体としてナビエ-ストークス方程式を基に考えるのか、水分子の運動をランダムウォークとして確率過程を考えるのか、それ以外のモデルを考える必要がのか、わかりたいレベルでさまざまなモデル構成の方法がありえます。津波のでき方を調べたいことが目的で、量子力学のモデルを構成して世界最速のスーパーコンピュータで計算してもあまり意味がないでしょう。水の場合は、物理の分野で非常に熱心に研究されてきているので、先行研究を調べることで様々なモデル化の可能性を調べることができますが、たとえば、生命の起源、言語の起源・進化、意識、心といった問題を扱おうとすると、そもそも基礎となる方程式や理論があるわけではないので、どのような問題(論理)をどのようなモデルの枠組みで考えられそうか、というところから考え始める必要があります。逆に、基礎理論がないからこそ、モデルを構成することができれば、問題点を明確化できるとも言えるかもしれません。
ここでモデルの枠組み(モデル化の方法)を知ることは構成的研究を進める上で重要だと思います。どういうモデルの枠組みを用いれば、どういうことがわかりそうかというヒントになります。例えば、上記の水分子の挙動を知りたいときにニュートン力学に基づいて古典的分子動力学法を用いれば、数ピコ秒から数ミリ秒の時間的オーダーで数千から数万の水分子の統計情報を得ることができるだろうし、量子力学に基づいて第一原理計算を行えばフェムト秒からピコ秒の時間オーダーにおける水分子間の水素結合の生成/崩壊の様子などを理解できるだろうと予想できます。他にもいろいろなモデル化の方法がありますし、新しく考えることも可能です。それぞれのモデル化の方法はそれぞれに利点と欠点があるのが普通で、一概にどれが良いということはできません。それぞれの研究の目的にあわせて選択する必要があります。逆にいろいろなモデル化の方法を通して、対象の理解が進むということができるでしょう。
一般的にモデルの抽象度が高くなればなるほど、分野を超えて、モデル間の比較ができるようになります。例えば、微分方程式は、星の運動にも化学反応にも人口増加の問題にも適用可能です。逆に言えば、他の分野で使われているモデル化の方法がまだ開拓されていない分野のモデル化にも応用できる可能性があるとも言えます。
4. 論理発見の効用
構成的モデル化では、構成途中の試行錯誤の過程で、副次的に多くの新しい論理が発見される可能性が考えられます。一般的に多自由度の非線形システムは初期値やパラメータ、また各要素の非線形性に依存して多様な振る舞いをする可能性がありますから、要素を入れ替えるだけ、パラメータを入れ替えるだけでもどのような出力になるか予想ができない場合が少なくありません。逆に言うと、常に「このような要素を入れたらどうなるのか?」と試し試しにやっていくことになります。それによって思いもよらない結果が得られる場合も十分にあり得ますし、そこから新しい論理を見いだすことにもつながります。これが橋本敬教授がいう「作って動かす」ということの二つ目の意味になると思います。また「構成的シミュレーションがアブダクションエンジンである」と言えるのはこの効用のため、と言えるかもしれません。例えば、金子教授らはカオス力学系を結合したGCM(Grobal Coupled Map、大域結合写像系)を構成して、カオス的遍歴現象(Chaotic itinerancy)など高次元力学系の新たな現象を見いだしました[金子研Web]。橋本敬教授はこのGCMも構成的モデルの一つとして紹介しています[knowledge02]が、(おそらく)はじめから「カオス的遍歴現象を実現するにはどうしたら良いか」という目的を持ってモデルを構成した訳ではなく「カオス力学系を結合したらどうなるのか?」という疑問があってモデルを構成して分析したら新たな現象が見つかった、というプロセスだったはずです(金子教授に直接聞いた訳ではないので確証はありません)。つまり、モデルを構成する過程で新しい論理を発見したと言えると思います。
5. モデルの定量性と定性性
「定量性」とは「Kg」や「秒」など具体的に物理単位で「量」を示せる性質のことで、「定性性」とはある量が「増加する」とか「振動する」などある量の変化傾向を示せる性質のことを言います。特に実験を重視するような研究者/科学者は具体的に測定器で何かを測ったり比べたりするので「定量性」を重視する傾向にあります。このことから「現象論的モデル」の場合には実際の実験と比較が可能な「定量的モデル」が良いモデルとされる傾向にあります。分子動力学モデルに代表されるように現象を定量的に再現する目的で作られるモデルは一般的にパラメータの数が多くなる傾向があります。そして時に現象を再現できるパラメータが「良いパラメータ」とされます。「パラメータ(Parameter)」とはシステムで使われる「定数」のことで、重力定数など理論、観察事実によって一意に決定されている定数から、計算時間や並列計算時の使用CPU数などユーザーが任意に決められる定数までいろいろ含まれます。とにかくここで言う「パラメータ」とは一回のシミュレーション(実験、計算)中に変化しない値のことを言います。
これに対して「構成的手法によって構成されるモデル」では「定性的なモデル」になる傾向があります。というのもこれまで述べてきたように、構成的手法は特にまだ発見されていない論理や機能を実現するモデルを示すことが主要な目的ですから、普通は定量的に現象を再現することよりも、定性的に機能を実現することを重要視する場合が多いからです。もちろん定性性、定量性を併せ持つもつモデルが構成されることに超したことはありませんが、構成的手法では、まずは定量性よりも定性性を重視する方が研究を進めやすいと思います。なぜなら構成的手法によるモデル化では、モデル構成を繰り返しながら、モデルの性質を網羅的に調べる必要があるのでパラメータの数が多いと現実時間的にモデルの性質を調べるのが大変になるからです。モデルの性質を調べるために良く行われるのが「パラメータサーチ」と呼ばれる作業で、これは網羅的にパラメータの値を振り直して、システムがどのようなパラメータ領域でどのような振る舞いをするのかを調べる作業です。例えば、上記の「カオス的遍歴現象」というのはGCMシステムの「定性性」のことでパラメータサーチによって発見されたと言うことができます。分子動力学モデルの場合は、普通パラメータの数が膨大になるので、よほどシンプルなシステムでない限り、網羅的にパラメータサーチを実施することは計算時間的に難しいです。分子動力学モデルの場合たいていは、温度や圧力といった実験装置でも変更可能なパラメータだけを変更可能な領域で変化させてシステム挙動を調べることになります。ユーリとミラーのアミノ酸合成実験においてもモデルの「定量性」よりも「定性性」が重要視されています。水、メタン、アンモニア、水素がそれぞれどれくらいの量の時にどんなアミノ酸がどれくらいできるか(定量性)、ということよりは、水、メタン、アンモニア、水素がある一定量存在していればアミノ酸が自然合成される可能性がある(定性性)、ということが主な主張点だと考えられます。
しかし、逆に定量的なモデルが構成的手法に使えないのか、というとそういう訳でもありません。分子動力学法の開発者のバーニ・アルダー(Berni J. Alder)らは、もともとは具体的な対象をモデル化したわけではなく、一種の「理想液体」のモデルを分子動力学法で計算をして結晶化の主要因が分子間の引力ではなく斥力(反発し合う力)である、といういわゆる「アルダー転移」を発見しました(分子シミュレーションによる結果から仮説として提示しました)[alder57][hiwatari07]。ここで使われた剛体球の分子動力学モデルは、現実にはあるはずの分子間の「引力」をなくし「斥力」だけにしたモデルで、圧力パラメータを変化させて、分子の結晶状態(秩序状態)を実現させました。そういった意味では定性性を重視した極力パラメータの少ないシンプルなモデルで圧力パラメータの違いによるシステム挙動を調べて、つまりパラメータサーチをして新しい論理を発見した、とも言えると思います。
6. 「やっこう研究」の危険性
試行錯誤的にシステムを構成してその振る舞いを調べることだけに注力してモデル構成の意義を深く考えないと、いわゆる「やったらこうなりました研究(やっこう研究)」に陥る可能性が高まります。何のためにそのモデルを構成するのか、何をわかりたいためにモデルを構成するのか、といったモデル構成の意義を注意深く考えておかないと、構成されたモデルの振る舞いや性質がわかったところで論文を書くことは難しいですし、研究の目的や、その研究が他の研究とどのような関係に位置づけられるのか、将来どのように研究を発展させていくつもりなのか、など答えることが難しくなります。やっこう研究では研究目的を要約すると「これこれをこのように構成するとどうなるのかわからないのでとにかくやってみます」となり、結論を要約すると「やってみたらこうなりました」となり、将来の展望は「もっと改良してみて調べてみます」となります。工学系の研究で何らかの手法の効率性を高めるというような研究であれば、あるいはこのようなスタイルでも可能かもしれませんが、そうするとそもそも「科学的手法としての構成的手法とは」ということを考える必要はないと思います。
7. 研究計画の立て方
構成的手法による研究計画を立てる場合の一つの考え方を書いておきます(この他にもいろいろ考え方はあると思います)。
まず研究目的ではこれまで述べてきたように
どのような論理を構成(検証)するつもりなのか
を述べるべきす。そして
その論理を構成する意義は何か
を述べる必要があります。純粋な数学的な解析や証明を目的にする以外には、興味の対象である分野において現在わかっていない「論理」が何であるかを具体的に示すのが有効だと思われます。例えば現象としては観察されているがどうして(何が原因で)それが起きているのかよくわからない現象の理解などが特に構成的手法による自然科学的研究の目的になり得ます。しかし、構成的手法による論理構築では、現実の現象に対して十分条件の提示しかできないことは明記しておくべきだと思います。例えば「モデル構築によって現実に起きている○○の動作メカニズムを解明する」などと述べるのは構成的研究の過大評価になる可能性があります。例えば、セルオートマトンによる自己複製のモデルを解析したからといって、DNA分子の複製メカニズムを解明したことにはならない、ということです。言えるのは複製メカニズムの十分条件を示せる、ということですが、現在ではすでに分子レベルである程度DNA分子の複製メカニズムが明らかになってきているので、仮にフォンノイマンの研究がまだ発表されていなかったとしてもセルオートマトンのような抽象モデルで自己複製の論理を示したところで、生物学的意義はあまり大きくないでしょう(数学的には意義はあるかもしれませんが)。もしDNA分子複製メカニズムの未解明の部分を明らかにしたい、というようなことを研究目的としたいのであれば、分子生物学がある程度発展している現在なら抽象的な「構成的モデル」というより定量的比較が可能な物理学的化学的な「現象論的モデル」を構築して、実際の実験結果などの研究結果との比較を通して現象を説明するためのモデルを構築するべきだと思います。逆に未解決の論理、例えばDNAのような遺伝分子がない状態からどのように遺伝分子が誕生できるのか、というような問いは構成的モデルでその十分条件を示せる可能性があります。
研究のより詳しい説明の部分にはその論理構築に今現在何が足りないのか、必要なのか、どこまでの論理が構築されているのか、そこにどういう論理が足されれば実現しそうなのか、といった論理実現に向けた仮説を書きます。どのような先行研究に基づいているのか、またどのようなモデルの枠組みを用いるつもりなのか、その理由などを述べるとその論理の「実現可能性」が高まるかもしれません。図式的に端的に表現すると
A → (*) → B
の最終的に実現したい結論Bが何で、十分条件にあたるAが何で、この論理「A → B」を成り立たせるために必要な論理の部分 (*) がどのようなものでありそうか、という仮説になります。もちろんモデル構成の過程でもろもろの理由からその仮説(論理)が実現しないかもしれませんが「実現しそうだ」と思える説明が必要です。そして実際にモデルを構築することでその仮説(論理)が成り立つことを検証した、という仮説演繹法にのっとった説明をすることができます。あるいはその論理はこれこれの十分条件を使うことで成り立つ、と構成的に論理を証明することができます。が、実際問題として、最終的にその実現したい論理が完成しなくてもモデル構成の過程で副次的に違った論理や結論を何かしら得られる可能性は高いと思われます。
ここまでで説明してきた流れをまとめると「現実に起きている現象の未解明の論理を(抽象的なあるいは定性的な)数理モデルもしくは計算モデルを構築することで、その論理が成り立つ十分条件を示す」という科学哲学的スタンスですが、これは現在システム生物学やバイオインフォマティクスで主に行なわれているオミクス研究に代表されるようなデータ主導の研究の方法論とは異なります。ただし、どちらが良い悪いということではなく、ものごとのわかり方あるいはわかりたい対象やレベルが異なるのであって、これらは相補的に発展していくべきです。佐藤譲氏は次のように述べられています[sato10]。
「分子生物学や理論生物学の台頭がいよいよ予期される現代において数学者、数理科学者の役割は創成される続ける実験結果の整理整頓や、既知の理論体系の既知の現象へのあてはめにあるのではないだろう。重要なのは数理科学的に誠実なまなざしを持って、真に問う意義のある生物学の理論的問題を「創造すること」である」
構成的手法は新しい理論的問題を創ることに向いている方法論と言えるかもしれません。ただ、データの整理やデータマイニング、データベース構築が生物学にとって重要でないということでは決してなく、ダーウィンさんが行なったように博物学的なデータ収集の中から帰納的に新しい法則なり理論的問題を発見することも可能だと思います。純粋数学者というよりはむしろコンピュータ科学者がこれら博物学的なデータマイニングの方法を得意としているでしょう。科学的立場や役割、科学的方法論が異なれど、互いの方法論を理解して尊重して協調しながら相補的に発展して行くのが科学あるいは科学者として一番の理想だと思います。
■ 科学的世界観(機械論、要素還元論、全体論、システム論、複雑系)
ここでは、いわゆる16世紀から17世紀にかけての近代科学成立以降におけるものの見方、つまり「科学的世界観」についてざっとその歴史を振り返りながらざっと「科学の考え方」を考えてみます。いわゆる科学史および科学哲学についての知識は実際の研究活動を進める上で必ずしも必要とは限りませんが「科学とは何か」「科学的方法とはどういうことか」と考えることは「知るとはどのようなことか」「わかるとはどういうことか」といった認識論や知識論にも関係していることで、普段の研究活動において、より深い考察をしたり、よりメタな視点から自分の行なっている研究活動を省みることができるようになります。また、自分の行なっている研究においてどのようなことがわかって、どのようなことがわからないのか、ということを理解する手助けにもなります。科学それ自体は普遍性や客観性、論理性を追求して発展してきていると思うのですが、人間活動である以上、研究手法やモデル構築の方法、実験結果の解釈などには少なからずその個人のものの見方や解釈、広く言えば世界観が反映されていますし、その世界観にはその時代の人々の世界観が反映されているは免れられないことで、少なくとも論文を投稿して論文雑誌に載せてもらうためには、ある程度他の研究者/科学者達と共通の世界観を持つ必要があると思います。また、異なる分野であったり違う世界観であっても理解し認め合う理解力が要求されます。
いわゆる近代科学の成立は16世紀から17世紀にかけてルネ・デカルト(1596 - 1650)、ニコラウス・コペルニクス(1473 - 1543)、アイザック・ニュートン(1642 - 1727)、ゴットフリート・ライプニッツ(1646 - 1716)、ヨハネス・ケプラー(1571 - 1630)、ガリレオ・ガリレイ(1564 - 1642)といった方々の業績に依るところが大きいでしょう。デカルトは「近代哲学の父」と呼ばれており「近代科学」の基礎を築いた一人であることは間違いありません。特に「方法序説」という著書に記されている4つの規則、明証、分析、統合、枚挙の考え方は近代科学の考え方の基礎といっても良いかもしれません。またデカルトは精神(心)と身体を分離して考える心身二元論(物心二元論)を唱えました。精神以外のものは広がりをもつものととらえ、そこから空間をx,y,zという座標で表現する方法を着想したことでも有名で「デカルト座標」と言われています。従来の科学はこのような二元論的視点から主体と客体とを分けて考えることが基本であると言えます。そして客体として観察できる物は古典力学的な因果関係の連鎖で決定論的に解釈できるという機械論的自然観を提唱してその後の科学者に大きな影響を与えました。ニュートンもその一人で、その考え方はニュートン力学に顕著に見て取れます。しかし、このデカルト流の考え方(デカルト主義)は、対象をできるだけ細かく分解して、その要素の性質に還元して物事を理解しようとする要素還元論に向かう傾向があります。その結果、分子、原子、素粒子と研究対象がどんどん細かくなっていったのは物理学の歴史をみてもわかります。
ところが多種多様な多数の要素が非線形的に相互作用し合う生物のようなシステムは、単に構成要素の性質を足し合わせるだけでは説明できないことが多いことがわかります。システム全体の性質を要素の性質と要素間の関係性によって説明しようとするのがいわゆるシステム論で、ルートヴィヒ・フォン・ベルタランフィー(1901 - 1972)らによって形成され、全体論(Holism)的な見方の必要性が見直されました(一般システム理論)。この全体論的視点からサイバネティクスや構造主義といった概念が生まれました。しかし、全体論的な見方はデカルト以前にもすでにあり「全体とは、部分の総和以上のなにかである 」という言葉はアリストテレス(BC384 - BC322)の言葉だとされています(還元主義(Wikiペディア))。それと同時にいわゆる非線形科学も発展し、散逸構造(dissipative structure)や動的平衡(dynamic equilibrium)という概念が生まれました。
これらの「全体論+非線形科学」の流れから、20世紀の後半からアメリカのサンタフェ研究所を中心に複雑系(Complex Systems)の研究が世界的に広まり、力学系理論(Dynamical Systems)、カオス理論(Chaos Theory)や人工生命研究(Artificial Life)と相まって、科学の世界を超えて一時的な流行になりました。(語弊があるかもしれませんが)複雑系というシステムや分野の厳密な定義がある訳ではなく、一般的には全体論的視点に基づいた非線形科学の範疇に含まれると考えられます。ただ、橋本教授は従来の科学で前提としてきた二元論的分離の問題を指摘しており、複雑系の特徴して、1. 全体と部分の分離不可能性、2. 観測者と観測対象の分離不可能性、3. オペレータとオペランドの分離不可能性 、といった分離不可能性を挙げています[knowledge02](複雑系)。
金子教授はこの「全体と部分の分離不可能性」のことを「部分に分離してもわからないということはどういうことかと真剣に向き合うことであり、別な言い方をすれば部分から成り立つはずの全体が決まらないと部分の性質が決まらないという循環と向き合うことでもある」と表現しています[kaneko99]。例えば、細胞内の遺伝分子であるDNA分子は細胞の中にあって他の分子と相互作用することで遺伝分子として機能するのであって、細胞からDNA分子だけを取り出してきしまっては遺伝分子としての機能は失われてしまい、DNA分子がなくなった細胞は細胞としての機能を失なってしまいます。つまり、DNA分子がどのような機能を持っているかを調べるには細胞の中でどのように他の分子と相互作用していて細胞全体の中でどの役割を担っているかを調べる必要があり、DNA分子の機能をDNA分子(部分)を含む細胞(全体)と切り離して考えることは難しい、といったことに相当します。
また典型的には「自分(主観、主体)」が含まれるシステムは「観測者と観測対象の分離不可能性」の問題が顕著に表出します。例えば、主観性を観察しようとすると困ったことが起こります。現代の科学では客観性が重要視されるので、例えば誰かに自分を観察してもらって主観性を客観的に記述しようとすれば主観性が損なわれますし、自分で自分の主観をそのまま記述しようとすれば客観性が損なわれます。たとえば「私の気持ち」などといって一生懸命自分の思いを書きつらねてもすばらしいブログやラブレターにはなるかもしれませんが、科学的な論文にするには難しいでしょう。フォン・ノイマンが問題にした「自己複製」も自己が含まれているので自分で自分を観察するという自己参照(自己言及)の問題に直面します。自分を観察するという行為そのものがその瞬間の自分の状態を変更させてしまうので、自分の完全な記述は自分を観察し続ける限り永遠に得られません。これに対してフォン・ノイマンは「観測に対して安定な自己の記述」と「自己を複製する機械」という自己を分離するアイデアを用いました。しかし、(自己をどう定義するかにもよりますが)もし参照することで自己の何らかの状態が変化すると考えると、自己を参照するという行為を含む自己を記述することは難しく、自己が自己を観察する限り自己の記述は常に不完全なものになります。例えば、試しに「いまこの瞬間に自分が考えたことをどのように考えているのか」という自分自身の思考のプロセスについて考えようとすると、その考えようとした行為自体が考えることの対象になってしまうため、私たちはたちまち混乱してしまいます。また「自己を複製する機械」がない状態で、どのように「自己を複製する機械」を構成するのか、という問題はプログラミング言語のコンパイラやOSの起動時などにも見られブートストラップ問題と言われます。
数学においても似たようなの二元論的分離の問題があり、通常は演算子(Operator)と変数(数値)(Operand)を分離して考えます。例えば「3」という数値と「+」という演算子はどちらが大きいかとか、「+」と「-」を足すといくつになるのか、などと言ったことは普通は考えません。数理モデルを構成する場合は通常、このように変化可能な状態(変数)と状態を変更する不変の(演算)規則の部分に分離して対象をモデル化します。そのため、これらの状態と規則が相互に切り替わるようなようなシステムの記述には何らかの工夫をする必要があります。これらのオペレータとオペランドの拡張は、数学的には汎関数や作用素、計算論の分野ではラムダ計算などが有名で、プログラミング言語の分野ではラムダ計算を元に考えられた関数型言語とよばれる言語で関数を引数にとる関数を扱うことができます(高階関数)。関数(オペレータ)のダイナミクスを考える方法として関数マップ(Function Dynamics)[kataoka02]や関数シフト(Functional Shifts)[namikawa04]やAlChemy[fontana91]といった研究があります。セルオートマトンもオペレータとオペランドを融合して考えられるモデルになっています。関数マップや関数シフトといった研究もモデルを構成するという意味で構成的研究だと言われますが、上述してきたような自然科学への還元を念頭に創られた構成的モデルというよりはむしろ、もっと抽象化された「モデルの枠組み」として考えられると思います。
およそこの複雑系の流行と同時に構成的手法(構成論的手法)という方法が言われ使われだしたと思います。それは要素還元論的に調べてきた要素を今度は逆に組み合わせてシステムを作り上げることでシステム全体としての特徴を理解したい、という全体論的な視点からの自然な流れで生まれてきた方法であると言えます。そのためか、ある種要素還元論を批判するような形で複雑系と構成的手法がセットで語られることがときおり見られますが、要素還元的視点も全体論的視点もどちらも物事の理解には必要であるし、また複雑系は研究対象のことであり、構成的手法は研究方法のことであり、本来独立して語ることができるものです。人工生命研究に代表されるように組み合わせたシステムと現実に対比できる対象がない場合にそのシステムを作り上げることにどういう科学的意義があるのか、といった疑問などから、これまでもさまざまな議論が行われれてきて、一つは、上述してきたように「ある論理実現のための十分条件を理解する方法」だという認識がある一方で、金子教授が言うように可能な論理探求のためや普遍性クラスを提示するための方法だという見方があったり、また橋本教授が言うように複雑系の二元論的分離の問題を探求する一つの方法である、といった見方があったりと研究者/科学者全体で「構成的手法」についていまだ統一した見解には至っていないのが現状だと思います。
しかし、最初にも述べたように、構成的手法とは何かとか、あるいは、あるモデルが構成的モデルかそうでないか、といったことを議論することよりも、そのモデルは何を理解するために構成されたのか、というモデル構成の意義を考えることの方が実際に研究を進める上では重要だと思います。そのモデル構成の意義を考える一つのきっかけとして、構成的手法という見方で科学的研究手法を眺めてみると、また別の研究手法の利点、欠点などが見えてきて、モデル構成の意義を一歩深く考えることができるようになるのではないでしょうか。
■ 参考文献
-
[knowledge02]Web版ナレッジサイエンス知を再編する64のキーワード, 北陸先端科学技術大学院大学知識科学研究科監修, 2002
ナレッジサイエンス-知を再編する81のキーワード , 近代科学社, 改訂増補版, 2008
, 近代科学社, 改訂増補版, 2008
-
[arita09]人工生命モデルによる構成的研究の方法論,
有田 隆也, 人工知能学会誌, Vol. 24(2), 2009
-
[hash08]Evolutionary Constructive Approach for Studying Dynamic Complex Systems
Takashi Hashimoto, Takashi Sato, Masaya Nakatsuka and Masanori Fujimoto (2008)
Recent Advances in Modelling and Simulation, Giuseppe Petrone and Giuliano Cammarata (Eds.), pp. 111-136, I-Tech Books, 2008
-
[hash10]社会的知能発生学における構成論的シミュレーションの役割 と SIGVerse の開発
Role of Constructive Simulation and Development of SIGVerse in Sociointelligenesis
橋 本 敬, 稲 邑 哲 也, 柴 田 智 広, 瀬 名 秀 明
日本ロボット学会誌, Vol. 28(4), pp.407-412, 2010
-
[kaneko09]生命とは何か複雑系生命科学へ

金子邦彦, 東京大学出版会, 第2版, 2009
-
[yonemori07]アブダクション-仮説と発見の論理

米盛裕二, 勁草書房, 2007
-
[hiwatari07]アルダー転移50周年 : 分子シミュレーションの夜明け : 分子動力学とモンテカルロ・シミュレーション(<小特集>アルダー転移50周年)
,
樋渡保秋, 日本物理学会会誌, Vol. 62(10), pp. 738-743, 2007
-
[miller53]A Production of Amino Acids Under Possible Primitive Earth Conditions
Stanley L. Miller, Science Vol 117, pp 528-529, 1953
-
[kaneko99]複雑系としての生命システムの論理
金子邦彦, 物性研究 , Vol. 71(4), pp 618-625, 1999
-
[fontana91]Algorithmic chemistry
Walter Fontana, Artificial life II, Vol. 11, pp 159-209, 1991
-
[kataoka02]Dynamical Network in Iterated Function Dynamics (関数マップ)
数理解析研究所講究録, Vol. 1244, pp 172-180, 2002
-
[namikawa04-1]Dynamics and computation in functional shifts
Jun Namikawa and Takashi Hashimoto, Nonlinearity, Vol. 17, pp 1317-1336, 2004
-
[namikawa04-2]ルールダイナミクスを記述する枠組みとしての関数シフト
The 18th Annual Conference of the Japanese Society for Artificial Intelligence, 2004
-
[alder57] Phase Transition for a Hard Sphere System
B. J. Alder and T. E. Wainwright, The Journal of Chemical Physics, Vol. 27, pp 1208-1209, 1957
-
佐藤讓, オートマトンモデルの背景, 現代思想 9月号, 2010
■ 構成的手法を主な研究手法として掲げている日本の研究室
(順序は特に意味がありません)(随時更新中)
- 北陸先端科学技術大学院大学、知識科学研究科、橋本研究室、言語進化
- 東京大学大学院、総合文化研究科、金子研究室、複雑系生命科学
- 東京大学大学院、総合文化研究科、池上研、複雑系と人工生命
- 名古屋大学、情報文科学部、有田研、人工生命
- 大阪大学大学院、情報科学研究科、四方研、人工細胞
- 東京工業大学、大学院総合理工学研究科、木賀研、合成生物学
- 理化学研究所、合成生物学グループ、上田研
